智能空战方法思路

1.动力学模型

根据《飞行器控制系统》书籍可以得到如下关系式

• 力方程组

  $$\left\{\begin{array}{l} \dot{u}=v r-w q-g \sin \theta+\frac{F_x}{m} \\ \dot{v}=-u r+w p+g \cos \theta \sin \phi+\frac{F_y}{m} \\ \dot{w}=u q-v p+g \cos \theta \cos \phi+\frac{F_z}{m} \end{array}\right.$$

• 运动方程组

  $$\left\{\begin{array}{l} \dot{\phi}=p+(r \cos \phi+q \sin \phi) \tan \theta \\ \dot{\theta}=q \cos \phi-r \sin \phi \\ \dot{\psi}=\frac{1}{\cos \theta}(r \cos \phi+q \sin \phi) \end{array}\right.$$

• 力矩方程组

  $$\left\{\begin{array}{l} \dot{p}=\left(c_1 r+c_2 p\right) q+c_3 \bar{L}+c_4 N \\ \dot{q}=c_5 p r-c_6\left(p^2-r^2\right)+c_7 M \\ \dot{r}=\left(c_8 p-c_2 r\right) q+c_4 \bar{L}+c_9 N \end{array}\right.$$

• 导航方程组

  $$\left\{\begin{array}{l} \dot{p}=\left(c_1 r+c_2 p\right) q+c_3 \bar{L}+c_4 N \\ \dot{q}=c_5 p r-c_6\left(p^2-r^2\right)+c_7 M \\ \dot{r}=\left(c_8 p-c_2 r\right) q+c_4 \bar{L}+c_9 N \end{array}\right.$$

其中$c_1=\frac{\left(I_y-I_z\right) I_z-I_{x z}^2}{\Sigma}, \quad c_2=\frac{\left(I_x-I_y+I_z\right) I_{x z}}{\Sigma}, \quad c_3=\frac{I_z}{\Sigma}$$\begin{gathered}c_4=\frac{I_{x z}}{\Sigma}, \quad c_5=\frac{I_z-I_x}{I_y}, \quad c_6=\frac{I_{x z}}{I_y}, \quad c_7=\frac{1}{I_y} \\ c_8=\frac{I_x\left(I_x-I_y\right)+I_{x z}^2}{\Sigma}, \quad c_9=\frac{I_x}{\Sigma}, \quad \Sigma=I_x I_z-I_{x z}^2\end{gathered}$

$\left\{\begin{array}{l}\bar{L}=\dot{p} I_x-\dot{r} I_{x z}+q r\left(I_z-I_y\right)-p q I_{x z} \\ M=\dot{q} I_y+p r\left(I_x-I_z\right)+\left(p^2-r^2\right) I_{x z} \\ N=\dot{r} I_z-\dot{p} I_{x z}+p q\left(I_y-I_x\right)+q r I_{x z}\end{array}\right.$

关系式确定了状态向量$\boldsymbol{x}=\left[\begin{array}{llllllllllll}u & v & w & \phi & \theta & \psi & p & q & r & x_{\mathrm{g}} & y_{\mathrm{g}} & h\end{array}\right]^{\mathrm{T}}$与控制输入向量$\boldsymbol{u}=\left[\begin{array}{llll}\delta_T & \delta_{\mathrm{e}} & \delta_{\mathrm{a}} & \delta_{\mathrm{r}}\end{array}\right]^{\mathrm{T}}$之间的非线性函数的关系（？？？？），所描述的12个方程都是封闭的。只要已知飞行器相关的特征参数，再根据飞行高度$h$,马赫数$Ma$以及飞行状态，就可以确定力$(F_x,F_y,F_z)$和力矩$(\bar{L}, M, N)$

2.问题建模

2.1组合优化问题

需要解决的问题是构建不定长的$A_{aim}=\left{ a_1,a_2\cdots ,a_n \right} $决策序列来使飞行器之间的位置关系达到某种状态。

对于静态和确定环境，比如敌方飞行器按照固定模式进行飞行，所有信息已知进行快速求解。可以建模为一个组合优化问题

$$\begin{cases} \min f(x)\\ \mathrm{s}.\mathrm{t}. g(x)\ge 0\\ x\in D\\ \end{cases}$$

其中$X$为解空间，$f(x)$为目标函数。‘

2.2马尔可夫决策过程问题

但是由于本论文对方的动作是无法自己是无法得知的，是一个动态而且随机的环境，但是可以得知未来的状态可以由当前状态和动作决定。所以，将其建模为一个马尔可夫决策过程（MDP）问题。马尔可夫过程由一个4元组构成$(S, A, T, R)$

• $S$是一个有限集（是否意味着连续状态空间的算法会有问题？），其中每个元素代表一个状态
• $A$是一个有限集（是否意味着连续状态空间的算法会有问题？），其中每个元素代表一个行动
• $T$是状态转移函数，将每个“状态行为”映射为$S$的一个概率分布。
• R是回报函数，表示在$s$上执行$a$所得到的即时回报。

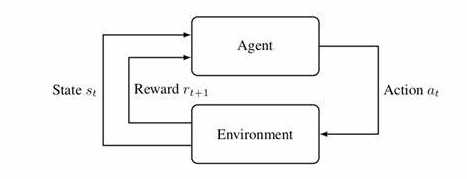
MDP问题的目标是求解最优策略让回报最大化。

3.问题求解