算法

第一章 算法在计算中的作用

算法定义计算过程，将输入转换成输出。
数据结构存储和组织数据。

第二章 算法基础

1 伪代码

• 缩进表示块(代替begin,end)
• for,while,repeat-until,if-else,to,down,by
• //(行注释)
• 数组元素通过[小标]表示，..表示范围(A[1…j])
• 复合数据表示为对象(A.length)

INSERTION-SORT(A)
    for j=2 to A.length
        key = A[j]
        //insert A[j] into the sorted sequence A[1..j-1]
        i = j-1
        while i>0 and A[i]>key
            A[i+1] = A[i]
            i = i-1
        A[i+1] = key

2 算法分析

最坏运行时间用$T(n)$表示
最坏情况用渐近记号$\varTheta$表示
插入排序：$\varTheta(n^2)$
归并排序：$\varTheta(n\log n)$

第三章 函数的增长

1 渐进记号

$\varTheta$渐近给出$T(n)$的上界和下界；
$O$提供了渐进上界时；
$\varOmega$提供了渐进下界。

• 对数:$\lg n=\log _2n$
• 多重函数：$f^{(i)}(n)= \begin{cases}n & \text { 若 } i=0 \\ f\left(f^{(i-1)}(n)\right) & \text { 若 } i>0\end{cases}$

第四章 分治策略

分治策略通过递归求解一个问题，通过三个步骤：分解,解决,合并。

递归式可以很自然得刻画分治算法得运行时间。
主方法：$T(n)=a T(n / b)+f(n)$ 表示$a$个子问题，每个子问题规模是原问题得$1/b$,分解和合并步骤总共花费$f(n)$。

还有代入法,递归树都可以用于求分治策略的复杂度

第五章 概率分析和随机算法

针对平均情况运行时间的计算，需要用概率进行分析。

第六章 堆排序(heapsort)

时间复杂度为$O(n \lg n)$

堆是一个数组，可以被看成一个近似的完全二叉树。

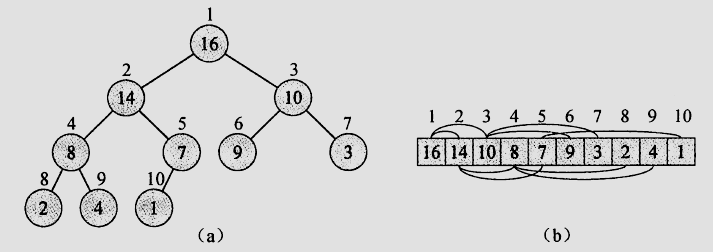
二叉堆由两种形式：最大堆和最小堆,最大堆中，父节点的键总是大于或等于任何一个子节点的键；最小堆中，父节点的键总是小于或等于任何一个子节点的键。

堆的一个常见应用就是作为高效的优先队列

第七章 快速排序

最坏时间复杂度$\Theta\left(n^2\right)$
但是平均性能很好，期望时间复杂度为$\Theta\left(n \log n\right)$

快速排序和归并排序一样用了分治的思想，

第八章 线性时间排序

前面的排序都叫做比较排序,任何比较排序在最坏情况下都要经过$\Theta\left(n \log n\right)$次比较

线性时间复杂度排序有：计数排序，基数排序，桶排序,这些排序通过运算来确定排序顺序

• 计数排序时间复杂度为