LSTM理论与实践

1.LSTM原理

---

设循环神经网络t时刻的隐变量可以表示为$\mathbf{H}_t$,其隐变量更新公式如下，

$$\mathbf{H}_t=\phi \left( \mathbf{X}_t\mathbf{W}_{xh}+\mathbf{H}_{t-1}\mathbf{W}_{hh}+\mathbf{b}_h \right)$$

其中$\phi$为激活函数，共有两套权重参数。分别为输入权重$\mathbf{W}_{xh}$和隐变量权重$\mathbf{W}_{hh}$。
RNN的输出可以表示为：

$$\mathbf{O}_t=\mathbf{H}_t\mathbf{W}_{hq}+\mathbf{b}_q$$

根据上述公式可以得到RNN的图示如下。

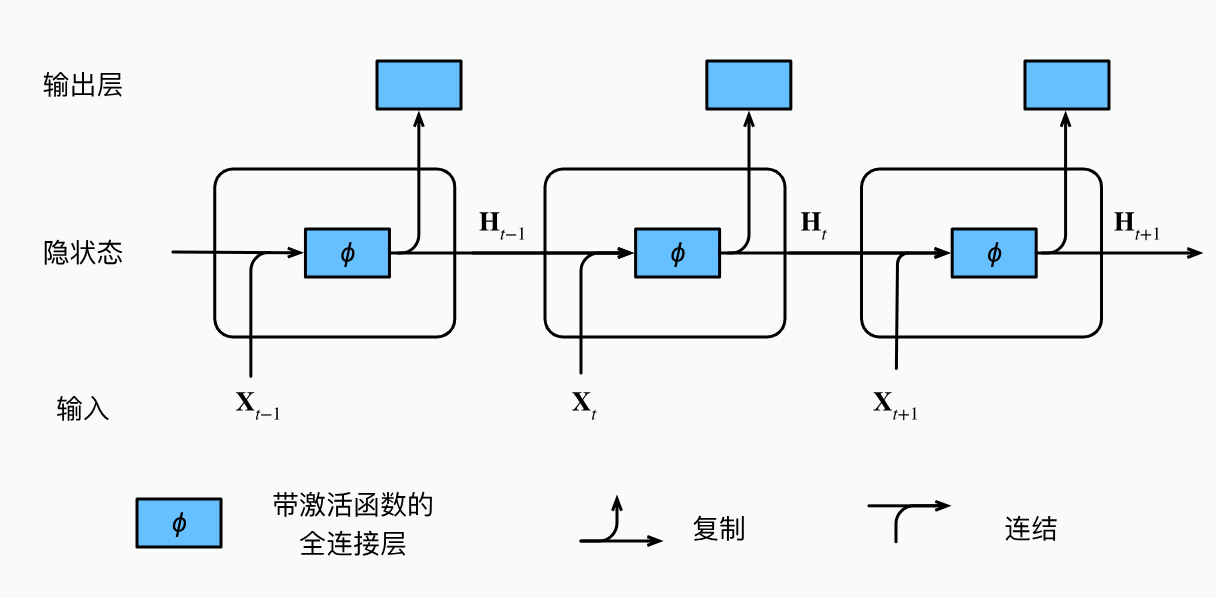
其底层代码实现如下：

假设$X$、$W_xh$、$H$和$W_hh$的形状为(3,1)、(1,4)、(3,4)和(4,4)。

import torch

def rnn(inputs, state, params):
    # inputs的形状：(时间步数量，批量大小，词表大小)
    W_xh, W_hh, b_h, W_hq, b_q = params
    H, = state
    outputs = []
    # X的形状：(批量大小，词表大小)
    for X in inputs:
        H = torch.tanh(torch.mm(X, W_xh) + torch.mm(H, W_hh) + b_h)
        Y = torch.mm(H, W_hq) + b_q
        outputs.append(Y)
    return torch.cat(outputs, dim=0), (H,)
def train_epoch_ch8(net, train_iter, loss, updater, device):
    state = None
    for X, Y in train_iter:
        if state is None:
            # 在第一次迭代或使用随机抽样时初始化state
            state = net.begin_state(batch_size=X.shape[0], device=device)
        else:
            state.detach_()
        y = Y.T.reshape(-1)
        X, y = X.to(device), y.to(device)
        y_hat, state = net(X, state)
        l = loss(y_hat, y.long()).mean()
        if isinstance(updater, torch.optim.Optimizer):
            updater.zero_grad()
            l.backward()
            grad_clipping(net, 1) #梯度裁剪，防止梯度爆炸
            updater.step()
        metric.add(l * y.numel(), y.numel())
    return math.exp(metric[0] / metric[1])